식을 간단하게 하고 간단하게 계산하기
보정계수 식을 보면 상당히 복잡해 보인다.
이 식에 어떤 숫자를 한번만 곱하는 거라면 모를까,
여러번 곱하는 것인 만큼, 간단하게 해줄 필요가 있다.
그리고 어떻게 간단하게 했더라도
어떤 식으로 간단하게 계산할 것인지를 파악해야 한다.
보정계수 식을 간단하게 하지 않으면
보정계수 구하느라 시간이 다 날아가고,
보정계수를 간단하게 했더라도
계산을 간단하게 하지 않으면 상당히 오래 걸리기 때문이다.
발문에 있는 조건 확인

여기서 확인할 수 있는 조건은
1. <수능최저학력기준> 통과
2. 최상위 1명만 선발
3. 국어, 영어, 수학 반영됨
먼저 이를 인지하고 접근해야 한다.
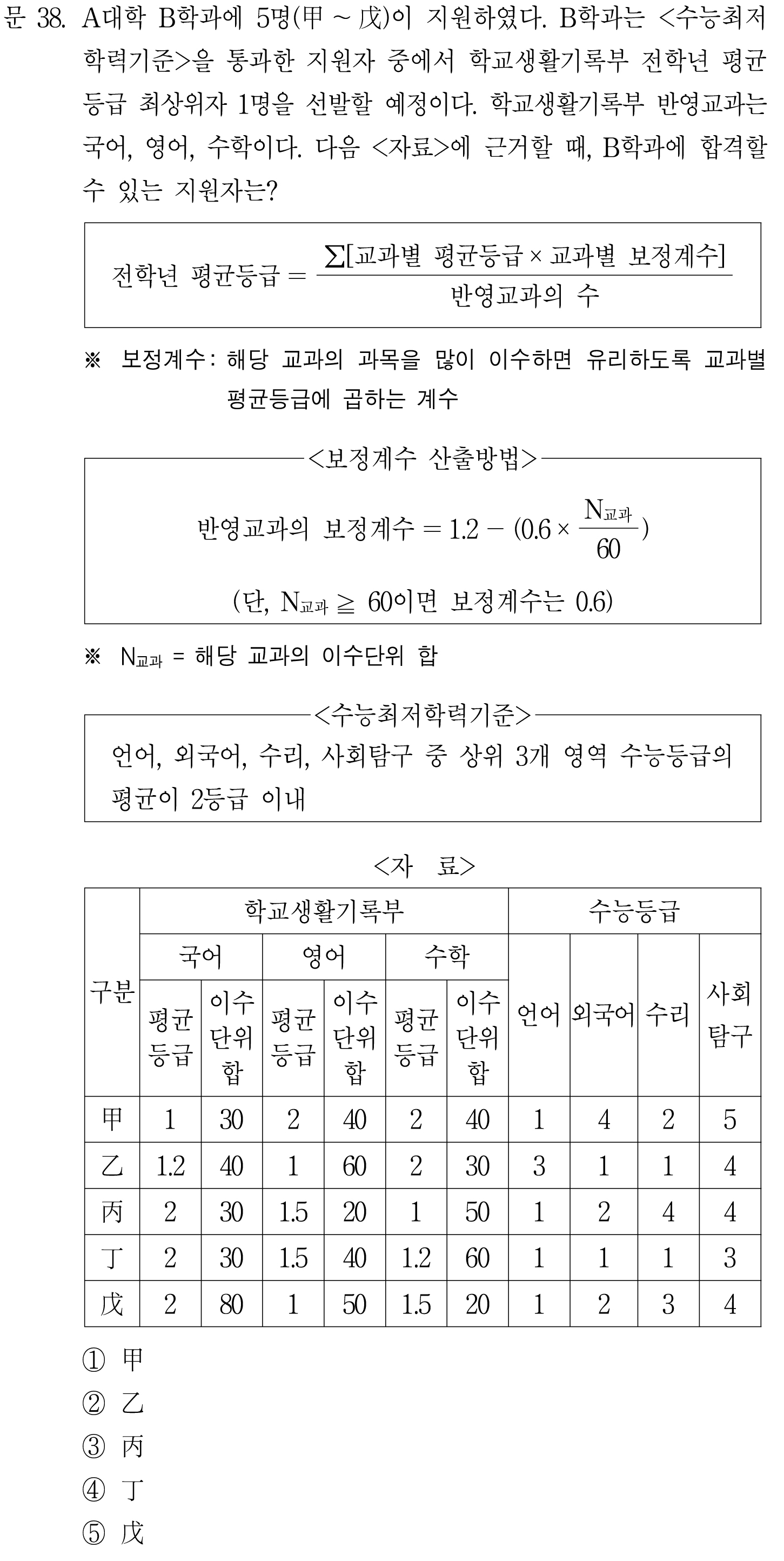
<수능최저학력기준> 통과하는 인원

수능 4개 과목 중에서 가장 잘 한 것 뽑아서 평균 2등급 안에 있는지 보면 된다.
그러니까 6만 안 넘으면 된다.
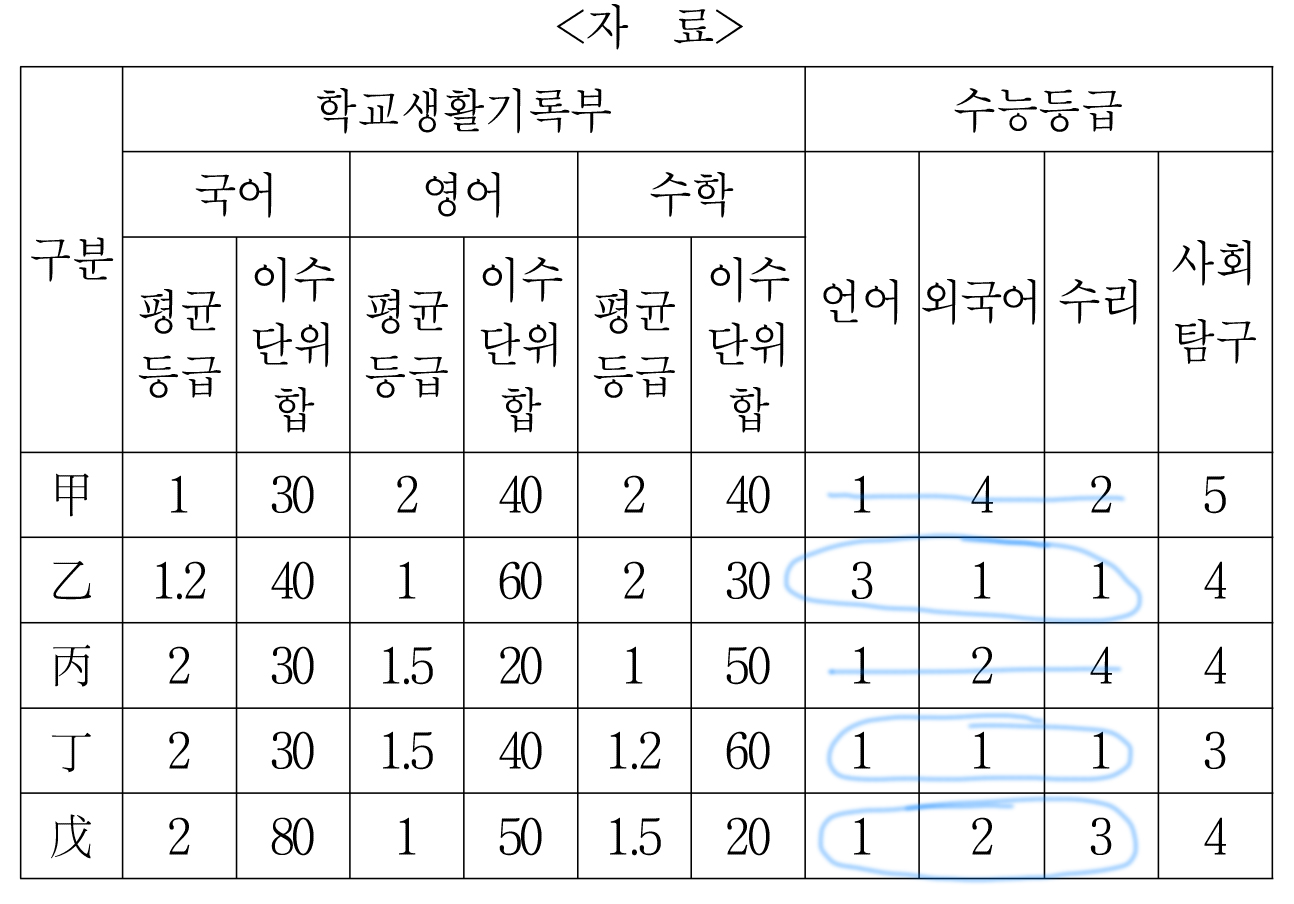
그러면 을, 정, 무만 남는다.
학교생활기록부 평균등급 최상위 1명

평균등급은 위와 같이 구할 수 있다.
교과별 평균등급은 이미 표에 나와 있고,
이제 보정계수를 구하면 된다.

일단 좀 복잡해 보인다.
간단하게 만들어보자

그럼 보정계수를 (120-N교과)/100로 바꿀 수 있다.
교과별 보정계수를 구해보자
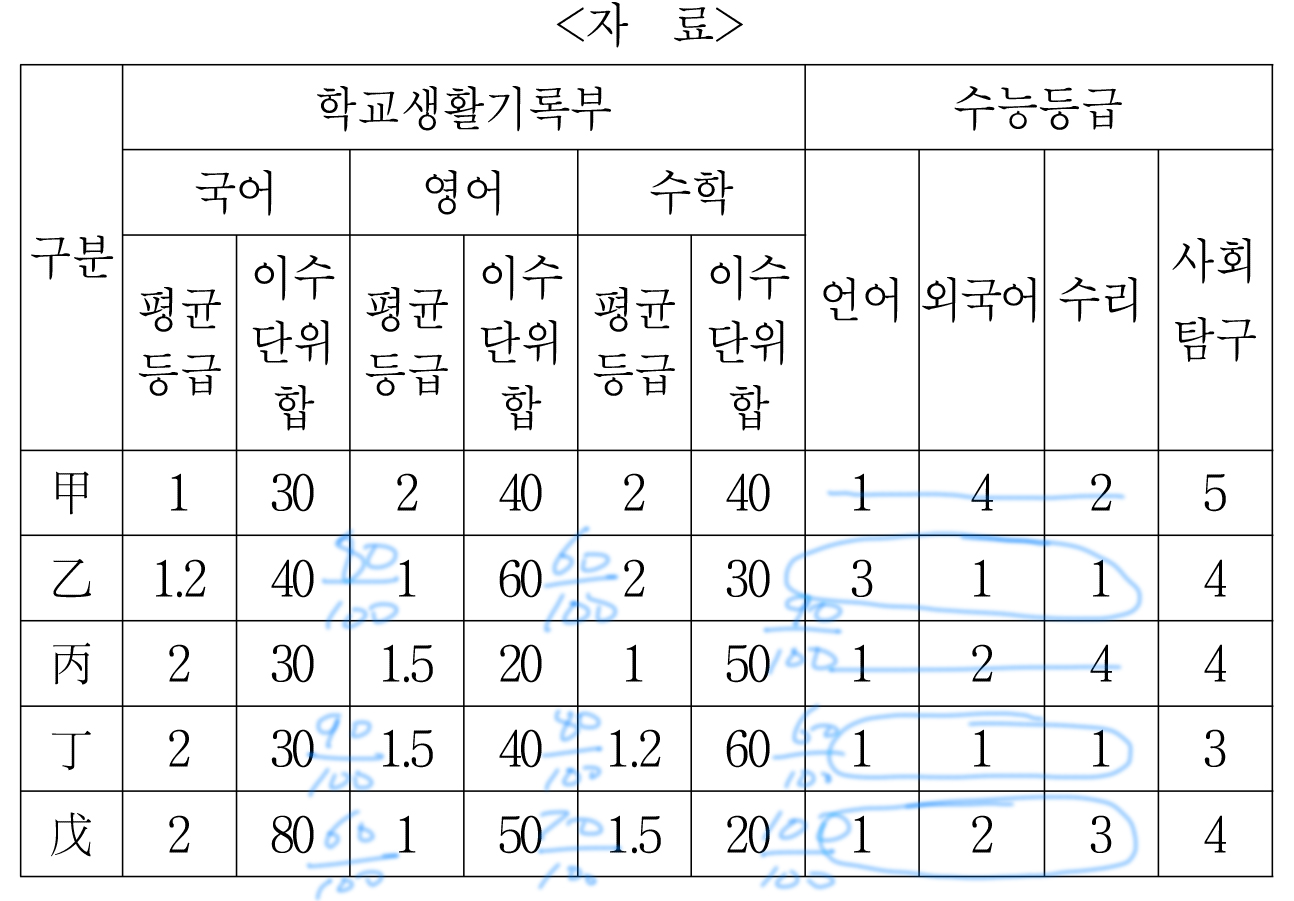
(여기서 중요한 건 이수단위 합이 60보다 크면 60으로 계산한다는 것이다)
그럼 이제 평균을 구할 수 있다.
어차피 분모는 3으로 같기 때문에 굳이 3으로 나눌 필요 없이,
분자가 가장 작은 걸 구하면 된다.
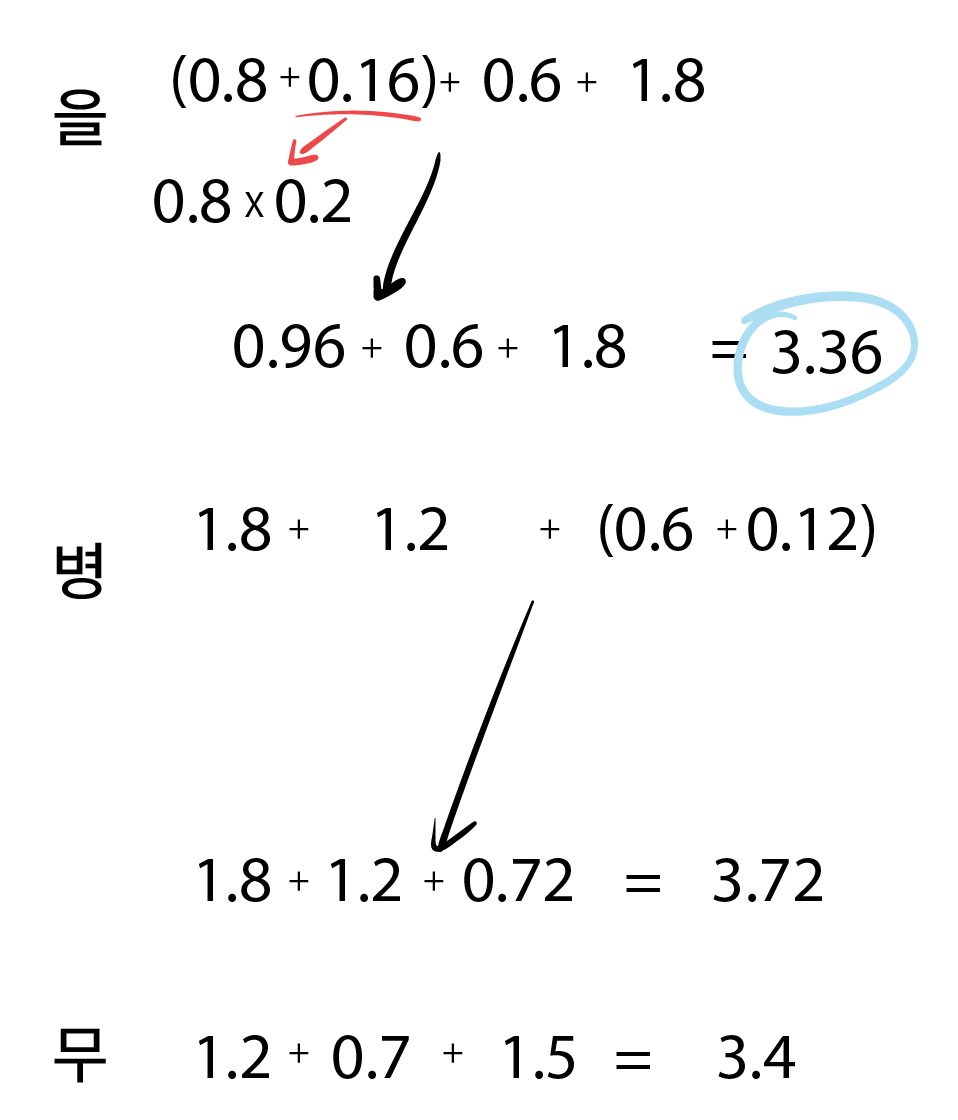
앞서 구한 보정계수에 1, 2, 심지어 1.5(그냥 절반만 더 더하면 되기 때문에)를 곱하는 건 문제가 안 된다.
문제가 되는 건 1.2를 곱하는 경우인데,
원래 것에다가 0.2를 한 것을 더하면 된다.
그렇게 해서 다 합하면
을이 3.36으로 가장 분자가 작다.
등급은 숫자가 작으면 작을수록 높은 것인 만큼,
을이 1등이라고 볼 수 있고, 그래서 을이 합격하게 된다.
답: 2번
'PSAT > 상황판단' 카테고리의 다른 글
| 2012년 5급 공채 PSAT 상황판단(인책형) 37번 오답풀이 (0) | 2025.01.30 |
|---|---|
| 2012년 5급 공채 PSAT 상황판단(인책형) 34번 오답 풀이 (0) | 2025.01.28 |
| 2012년 5급 공채 PSAT 상황판단(인책형) 32번 오답 풀이 (0) | 2025.01.28 |
| 2012년 5급 공채 PSAT 상황판단(인책형) 31번 오답 풀이 (0) | 2025.01.28 |
| 2012년 5급 공채 PSAT 상황판단(인책형) 30번 오답 풀이 (0) | 2025.01.27 |


